Knowledge Discovery Process for Blackbox Optimization
Traditional simulation-based optimization (SBO) approaches usually require pre-defined objective functions which directly describe the influence of all simulation input parameters on the specified simulation objectives (denoted as model behavior). Optimization toolsets, use these objective functions (e.g. ordinary differential equations) in order to find a local or global minimum which satisfies given constraints. As a consequence of the increasing complexity of state-of-the-art simulations within virtual testbeds, such objective functions are not always available. Even more, there are many technical complex systems whose long-term behavior can not be described by a set of equations (e.g. the behavior of autonomous systems in changing environments). This kind of SBO problem is called blackbox simulation problem because the objective functions are unknown to both: the simulation engineer and consequently optimization toolset. There is already a huge number of computational methods for solving multi-objective optimization problems (MOPs) which usually do not consider the generation of vast amounts of simulation model behavior results that can be derived from a knowledge discovery process (KDP) in simulations. Usually, the traditional approaches use heuristics of the unknown objective functions for their algorithms. However, these approaches converge much better to local or global minima when they are enhanced with additional information about the MOP. We propose for this purpose an approximation of the complete simulation model behavior.
In contrast to state-of-the-art approaches, which are not able to automatically analyze blackbox MOPs in simulations, our approach automatically builds an active model between simulation input and simulation objectives. This approximation of the simulation model behavior directly leads to an approximation of the feasible design space (FDS) of the simulation model configuration space for a Pareto based MOO.
|
| Our automatic knowledge discovery process: first, causal relations between simulation input parameters and simulation objectives are revealed. Second, simulation data farming is efficiently conducted in order to approximate the unknown objective functions and the FDS. These approximations are used in order to compute Pareto gradient information and solution. |
It uncovers unknown causal relations in large parameter sets between simulation input and model behavior which are assumed to be unknown non-linear objective functions. In detail, it approximates objective functions (resp. the FDS) in arbitrary deterministic and stochastic blackbox simulations as B-spline surfaces. It computes a Pareto gradient from this FDS approximation for concave, convex or interrupted Pareto fronts. In addition it is capable of computing an optimal solution from this FDS approximation via our hierarchical multi-agent-system (MAS) approach.
|
| The goal of our approach is to accurately approximate the unknown objective functions in order to formulate a FDS. Our approach conducts a dimensionality reduction of the high dimensional input space down to three-dimensional and two-dimensional representations of the unknown ojective functions for precise approximation. The gained knowledge about the unknown objective functions is then aggregated back to the high dimensional input space via our B-spline surfaces and FDS approximation. |
As our approach is completely automatic, it does not need any supervision from simulation experts. Another advantage of our approach is its performance. It gains its efficiency from a novel spline-based sampling of the parameter space in combination with a novel forest-based simulation dataflow analysis. Another main advantage of our approach is that our B-spline surface based FDS approximation evaluation is computationally very fast and replaces costly simulation evaluations which are usually required. Consequently, our approach also delivers a performance boost when computing a solution for the given MOP. Furthermore, our approach is very generic. It can be easily incorporated into existing SBO approaches which already use a KDP. Even more, the computed Pareto solutions are close to the Pareto front for both, deterministic and stochastic simulations. Another advantage of our approach are the provided optimization strategies. These strategies can be used by state-of-the-art MOO solvers in order to investigate a larger bandwidth of the simulated model behavior.
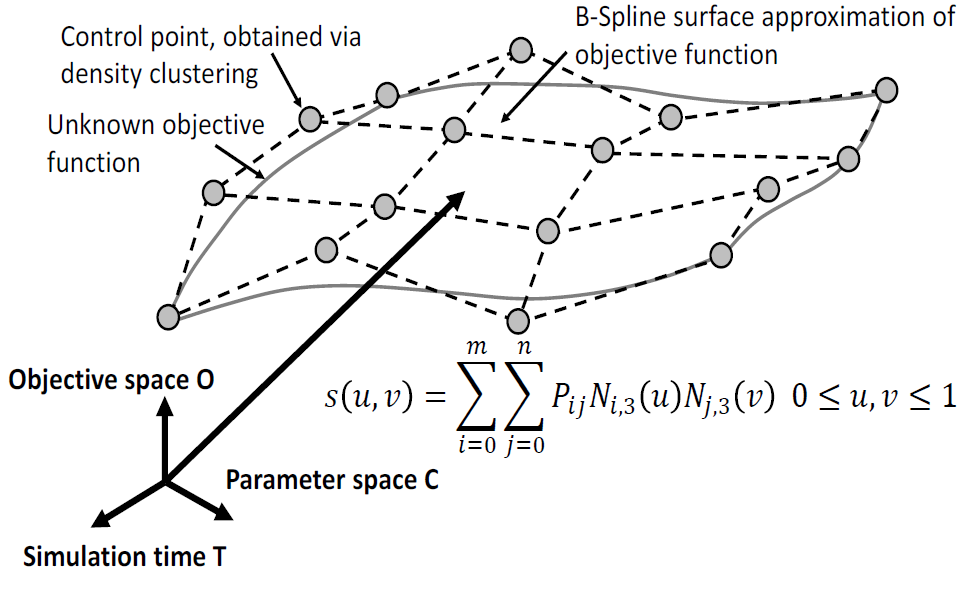
|
| B-Spline surface representation of the three-dimensional space constructed by simulation input parameter C, simulation time T and objective function space O. |
In order to utilize our proposed FDS approximation for computing an optimal simulaton model configuration solution, we developed a highly parallel optimization system based on our wait-free data management. The optimization system proposed here is based on a hierarchical MAS which aims at dynamically tuning all given input configuration parameters with respect to the approximated FDS, which is retrieved from our KDP. Such hierarchical MAS have already proven their feasibility for solving MOP. Our main idea is that every agent introduces a part-wise modelling single-objective optimization (SOO) and multi-objective optimization (MOO) constraints per input parameter) of the problem and its behaviour and communication to other agents is used to solve the global (MOO) problem. Instead of using a costly evolutionary approach, our MAS directly utilizes our cost-efficient FDS approximation and can converge much quicker to the solution.
Our MAS is composed of several agent organizations. Each of these organizations aims at optimizing a subset of configuration parameters for one or more simulation objectives, each one represented by our FDS approximation. These agent organizations are defined per specified simulation objective and consist of a hierarchy of two agent types: objective- and negotiation-agents. For each identified input parameter, one objective-agent is defined. The goal of every defined objective-agent is to maximize or minimize every attached simulation objective under Pareto constraints. Several optimization constraints arise because of the underlying MOP. Therefore, a negotiation-agent is defined for every specified objective. The goal of every negotiation agent is to manage requests between the objective-agents in order to satisfy the existing multi-objective constraints between the objective-agents. Our MAS is based upon our ECS based, wait-free, massively parallel data management approach. Consequently, all agents can communicate and exchange data very quickly, increasing the overall performance of the optimization process. Additionally, agents can be added and removed at runtime to the optimization system without the need of restarting the optimization run because it utilizes the ECS pattern.
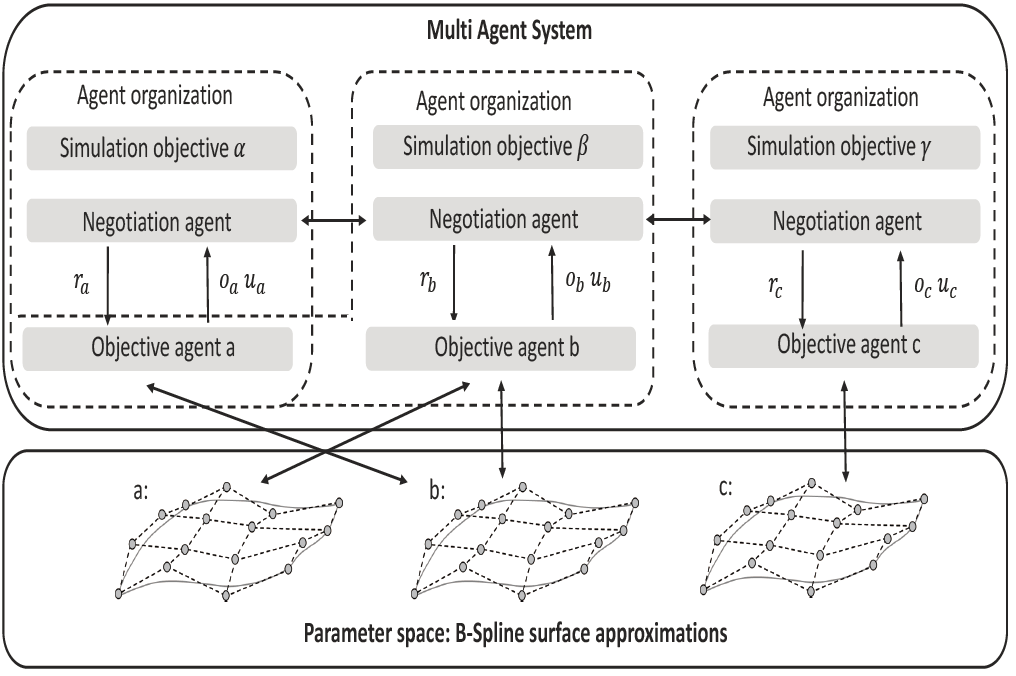
|
| Our MAS based optimization approach for a mixed objective problem statement (one multi-objective objective (beta) and two single-objective problems (alpha, gamma) with three input parameters): Each agent organization optimizes the parameter set for one objective. Negotiation agents handle requests between the objective-agents in order to effectively find the optimal parameter configuration. |
Results
|
|
| Our GDS approach outperforms its competitors for approximation error (left) and overall sampling rate of the input space (right). |
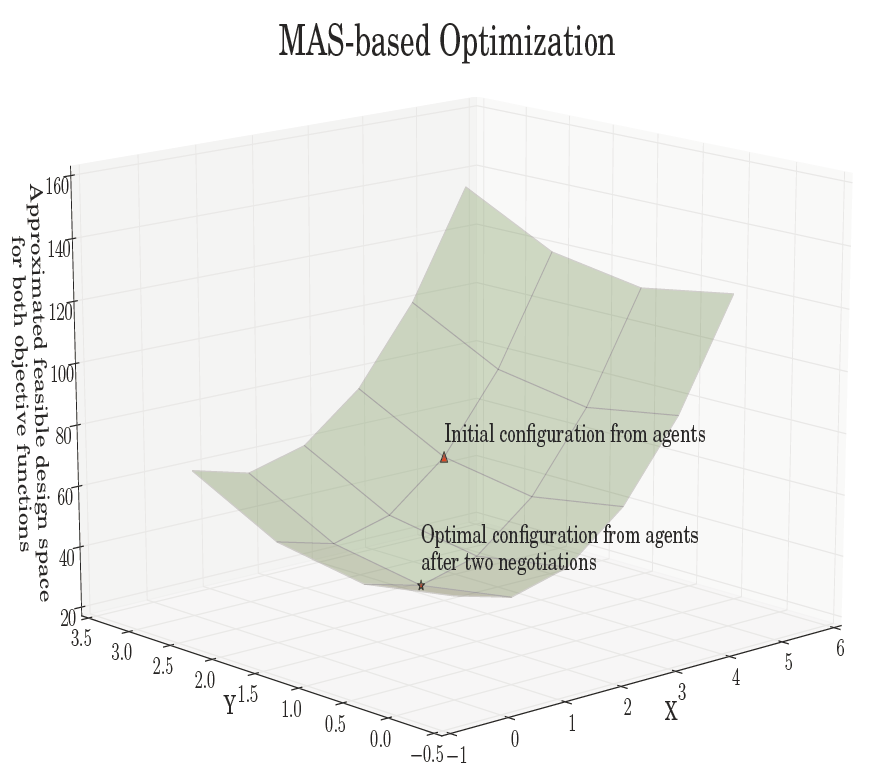
|
| Evaluation of one of our use case studies: Our agents are directly initialized at the single-objective solution and converge fast to the multi-objective solution for a given multi-objective optimization problem. |